Running the Tangents in a marathon can shave minutes off your time. Although the length of a marathon is commonly known to be 26.2 miles, this is only true if you follow the shortest legal route possible. The course is measured along its shortest possible route, referred to as the route line. When the course is measured and laid out a small amount of padding is built in to ensure the course complies.
Follow this link to see the USTAF guidelines.
With GPS tracking, many runners found they were running more than 26.2 miles. Some people were seeing as much as an additional half mile or further. At first, GPS was blamed for the inaccuracy. Then, some blamed the people who measured the course.
While there is a slight margin of error in GPS accuracy, the primary issue lies in the running habits of many, including the Elites, who often do not follow the shortest possible route.
What is a tangent?
The aim of running a marathon is to stay as close to the tangents as possible. But, what are tangents? They are the shortest lines possible between two points. The only reason to deviate from the route line is to get water, avoid traffic, or run on a better surface than the tangent line. However, many people are unaware of the route line and end up running much further. This extra distance can adversely affect their time. By running a marathon course correctly, it is possible to shave off anywhere from 3 to 5 minutes or more from your time compared to runners who stay on the center line.
Take the New York City marathon, for instance. Once you enter Central Park, there are 46 turns. People not running the tangents can add around two to three seconds per turn. For this section of the race alone, you can add as much as 2-3 minutes, depending on your pace! Many runners tend to stay on or near the center line for the entire race. Even when there is a 90-degree turn where the inside curb is 30 feet away, they still tend to stay on or near the center line.
After the L.A. race, some runners complained that the course was too long. Instead of the standard 26.2 miles, some runners had readings of 26.50-27 miles. This meant these runners ran an extra 1/3 of a mile because they did not run the tangents. On average, most runners add an extra 0.3-0.5 miles over the course of a normal marathon. This means a runner who averages 10 minutes/mile will run an extra three to five minutes because of the extra distance. Don’t be one of those runners who needlessly adds additional time.
Examples
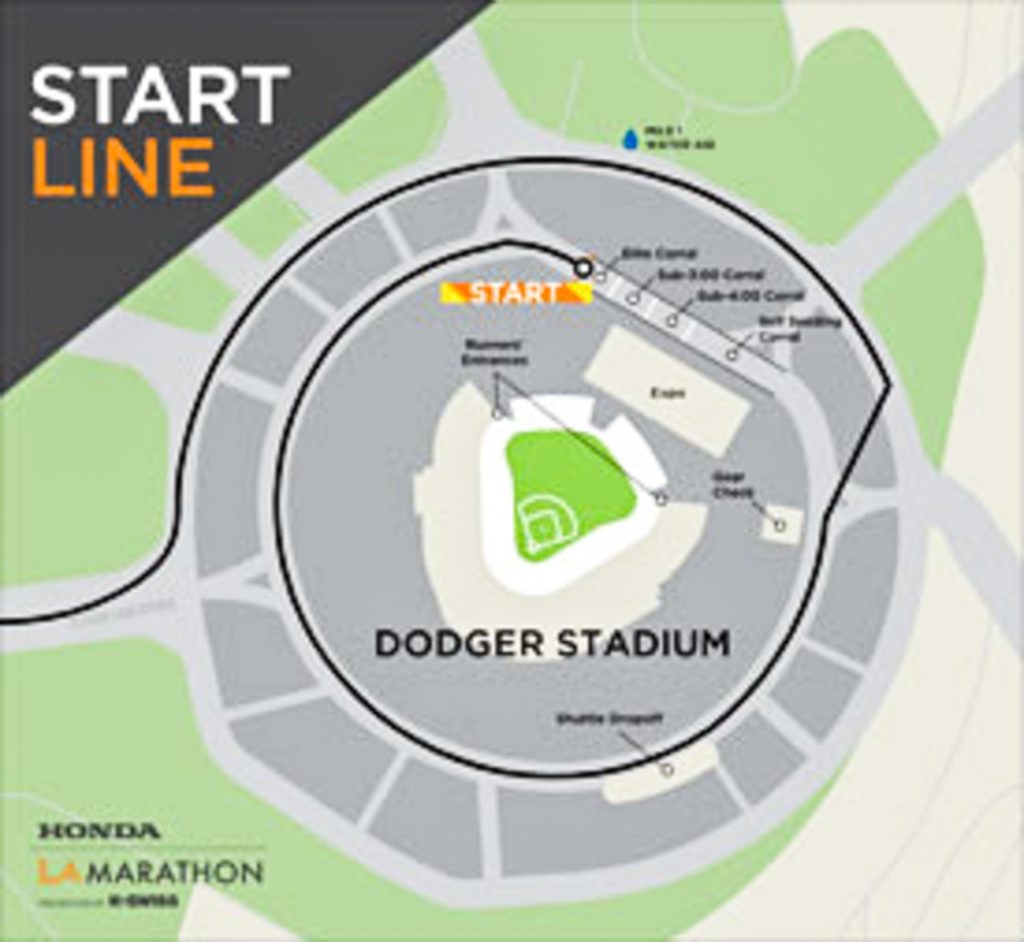
This is a map of the first mile of the LA marathon after they had changed the start to the Stadium Course. (It has since changed)
The width of the road was about 80-100 feet wide. Many people ran an average 60 feet from the inside line for the entire mile. This adds an extra 376 feet just in the first mile. For a person running a ten minute mile, this would add an extra 42 seconds.

In this photo, we can see runners making their way up Temple Street during the L.A. marathon. Once they reach the bottom of the hill, they turn right onto Temple Street, and at the top of the hill, they make another right turn. This street is approximately 80 feet wide. As a result, the runners on the right-hand side of the photo end up running an additional 160 feet in just a few short blocks. If these runners were maintaining a 10-minute mile pace, this extra distance would add approximately 18 seconds to their overall time. Therefore, to run the most efficient race, it is advisable to stay as close to the right curb as possible.
How to run the Tangent.
When running on a curved road, the closer you are to the inside of the curve, the shorter the distance you need to travel. For instance, when taking a right turn, it is best to be on the inside of the turn. Most roads have multiple curves. If there are two curves in opposite directions, then it is ideal to be at the apex of the first turn and look ahead to see where the top of the next curve is. Once you reach the top of the first curve, stay on the inside until you see the top of the next curve, and continue this pattern for each subsequent curve.
